Textbook Authors Must Be Careful That the Reading Level
Question
Textbook authors must be careful that the reading level of theirbook is appropriate for the target audience. Some methods ofassessing reading level require estimating the boilerplate give-and-take length.I’ve randomly called xx words from a randomly selected page inourtextbook and counted the number of letters in each word. Theresults are shown below:5, 5, 2, 11, 1, 5, three, 8, 5, four, 7, 2, 9, four,8, 10, 4, v, half-dozen, 6a)Construct a 98% confidence interval for the hateful length ofwords in our textb)Suppose we wanted to
Textbook authors must exist careful that the reading level of their book is advisable for the target audience. Some methods of assessing reading level require estimating the average word length. I’ve randomly chosen xx words from a randomly selected folio inour textbook and counted the number of letters in each word. The results are shown below:5, 5, two, 11, 1, v, 3, 8, 5, iv, 7, 2, ix, four, 8, 10, 4, five, 6, six a)Construct a 98% confidence interval for the mean length of words in our text b)Suppose we wanted to judge our texts mean word length to within 0.five messages with 98% conviction. How many randomly selected words should we use?
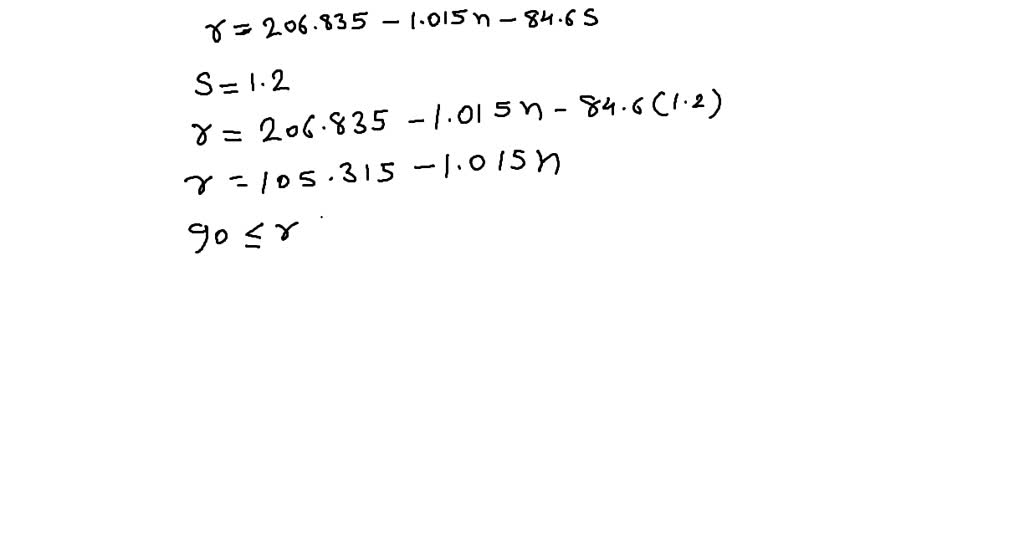
Answers
The reading difficulty of a textbook can be estimated by the Flesch Reading Ease Formula
$$r=206.835-1.015 north-84.6 southward$$
where $r$ is the reading ease, $n$ is the average number of words in a sentence, and s is the average number of syllables in a word. Sample reading-level scores are shown in the post-obit table.
$$\begin{array}{c|c}
\hline \text { Score } & {\text { Reading Ease }} \\
\hline 90 \leq r \leq 100 & {5 \text { th grade }} \\
{60 \leq r \leq 70} & {8 \text { th and } 9 \text { th grades }} \\
{0 \leq r \leq 30} & {\text { Higher graduates }} \\
\hline\cease{assortment}$$Bryan is writing a book for 5 th-graders using an average of one.2 syllables per word. How long should his boilerplate sentence length exist?
Flash reading East formula are equal. Practise 206 point 8 to five, minus one.0 15 time and minus 84 56 times as we're always a reading ease and and is the average number off globe in a sentence, equally is the average number off the levels in a world for at and ix grades, Alexa average 8 words per sentence, so it means an equal toe. Viii. Now we substitute that value in this formula, and we get our record. Do 206 indicate 85 minus 1.xv dying it minus 84 bespeak six Time as off. Resolving this we get commodity do 198 point 715 minus 80. Absurd detect six time. As for the eighth and ninth form, it is given sample reading level schoolhouse, which is 60 less than and equal toe are less than and equal to 70. Now information technology's bent the value of our in this and we get sixty less than and equal to 198 bespeak 71 Fight minus 84. Find six dime ads less than an equal to 70 subject 198.75 from all of 3 regions and we get minus 138 0.71 fight less than and equal to minus 84 0.6 times every bit less than an equal to minus 128 points. So one fight? No, we practise wait all off to organized religion by minus 84.six and flip the aforementioned. Then we become one.6 greater than an equal to as greater than and equal to one point fight, too. So the average number of syllables forrad between one.62 ane point fight, you can write similar that. 1.52 less than and equal s less than an equal practice 1.6. So that is ever final answer.
And so we're going to assume That the mean number of words per folio is actually 48. And alternately That at that place are more than 48 words per folio. And nosotros get an X. Bar of 53.3 words with a standard deviation Of 15.7 and the sample size was 10. And so we want to find, we're again we're assuming that it's 48, I similar to draw a picture And nosotros're getting 53.iii and we want to know is this significantly higher so that we have evidence against the nothing. Then we want to know what'south the likelihood of getting an X. Bar. If the hateful is truly 48, What's the likelihood of sampling 10 words getting the mean and having it exist 53.iii or college? So nosotros need to convert that to our test statistic. Our test statistic will be a T value with 9° of liberty and we take that 53.3 minus the hateful, divided by the standard deviation over the square root of N. And that's going to give u.s.a. our test statistic, Our our test at. And then let'south put this in the computer. Okay, that divergence looks like v.3 to me. So five.three divided by left parenthesis. E 15.7 divided past the foursquare root of 10. Okay. Yeah. And almost done here and I get that. That test statistic is one.6752 and it keeps going on and on. But I have that value in my figurer and I can look this upwards in a table. I can as well observe the critical Zeev a R T value for one% significance level. But I'm going to utilise find the actual p value for this. Then we want to find that surface area. And so I'm gonna use my software, I could look it upward in the table and find approximately between two values just might likewise simply utilize my calculator and nosotros're going to plug that. And as the lower this value will be my lower in my T. C. D. F. And and then 2nd answer. And and so I'm going to accept the upper be just a big T. Value. Like k could be at 100. And our degrees of freedom is just ix. And well I'one thousand sorry aye of degrees of liberty is nine. And when we practice that we find out that P value comes out to be .1567. And so nigh sixteen%. Now this number is larger than one past a lot. So nosotros fail to reject the zip. Mhm. So nosotros don't have evidence that uh nosotros take This seems to be consistent with the distribution that has a mean of 48, and if we have 48 times it said there were i,459 that comes out to be about 70,000 words. Then We would say that 70,000 words does seem to be consistent once again. That's that Number of pages, which was 1,459 times the average of 48. This seems to exist correct. Okay. Yeah. I guess we don't accept any evidence to say that the mean this 53.3 is college than 48, simply it doesn't appear to be significantly higher.
Lots of sections. That mitt mainly just bow tin s in this particular trouble. 10 is the length of one enquiry paper. Ah, Part B. Uh, says I pull of the, uh, ex is a uniform distribution on its from ten to 25. That'southward how nosotros even talk about the distribution. Okay, Part C, because the mean of Ten, uh, ask for the mean of X And since the mean, since it's uniformly distributed, ah, then the mean is just gonna be halfway betwixt 10 and 25 Eso the main is gonna exist 17.5 pages. Uh, office D. Every bit for the standard departure, okay. So and so the standard deviation is gonna exist the departure for a uniform distribution. It's just gonna be the difference in our largest and smallest and and then divided by the foursquare root of the number of samples due south that'southward gonna be fifteen divided by the square root of 55. Nosotros should be close. Teoh the calculator ii.2 to 6 uh, pages. Okay, and then eastward disaster in words describe explore is sexual activity bars only the mean length of a research paper for the boilerplate length of a research paper. Okay, uh, considering the part f simply wants us to. I described the mean into the hateful Should be normally distributed with a mean of 17.5. Uh, with standard error of I would see. Should exist that 2.2 to vi. Uh, divided by 55. Yeah, I believe then. Okay, speak up, then. The calculator. It is gonna be 0.37 Okay, Org. Okay. Part G. I just asked him words. What is the summation of X? And that merely means the full number of pages enquiry pages. Okay, uh, h age wants usa to actually calculate information technology. So h will be distributed A ordinarily, simply it's gonna be 17.five times 55 because we have 55 researchers. It's simply gonna be 962.5 pages on the standard deviation is 2.2 to 6. Eso if we multiply that by 55. Uh, information technology should give us a standard deviation of 111 pages. Okay. It'south ah, uh, function I says without doing any calculations. Do you think information technology'due south likely they'll need to read a full of more than 1000 l pages on. I would say yes because, um, if within only one standard deviation we are ah, at 1015. Um, so because 1050 and you can calculate similar a z score on that eso the Z score would be less than 1 eso It'southward inside one standard deviation of the primary. So I'd say it's pretty probable, um, so yep, Of pretty? Yes, information technology'south probable. Okay. Uh, J says kind of the trouble. The professor will demand to read a total of more than 1000 50 pages. Okay, so we're really I don't have to use a z table for that. Eso nosotros're gonna do m fifteen uh, minus 9 62.five and then divided by 111.243 Okay, proficient. Put that in the calculator. 2050 minus 9 62.5 divided by 111 point. Shoot for three. That's gonna give united states a Z score of 0.78 65 or 66 eso, which implies, may just accept to look that up on a Z table. Okay, Then that Z score, I gives a percentage of 78.42 But we want higher up that. So the right answer for that 1 would but be 100 minus that which is 21.575 twenty-four hours. There'southward a 21.58% take a chance that he reads more than than 1000 50 pages. Okay, says why is it, different the average length of the papers will be less than 12 pages. And so considering they're uniformly distributed between every page, number has a chance. United states of america. That means from ten to 25 uh, everything has an equal chance. So the fact that that if the average woodland so close to 12 um, that'south merely gonna requite it's just similar, highly unlikely that the pages would be all linked 12 if it's equally likely to be 10 through 12. Um, and since the lowest is is 10 we tin can't, um, for the average to come out to be 12 like nosotros can't accept very many papers above 14 eso. That's why because 12 is just so close to the bottom of finish. Okay, thank you very much.
All right, And then we are going to do this problem without having to use based theorem or even using a tree diagram. We just utilize a visual and then you lot have all the information. We put it together and exit. And so the visuals are very important in mathematics. So let'due south begin in the table off seasons text. Okay, then you're told in the four they used means professor of man's textbook. In the winter, they used millions textbook, and in the spring in the spring they used Professor Moz textbook. Okay. And then we also told about satisfaction. We're told that out of the 500 students who used ways textbook, only 200 was satisfied, significant that 300 watt and satisfied. And so out of the 300 who used Professor Medians book handed on 50 was satisfied, significant that 150 we're not satisfied and 200 used. Professor Moore's book 160 was satisfied, pregnant that the remaining twoscore were non satisfied. At present these numbers are very important. So 200 simply tells y'all that these other students who used profits on Maine'due south volume and they want satisfied and this number hither tells you that 100 and 50 students used Medians book and they were satisfied. And finally, these number tells y'all that these are the students who used Professor Moore'southward volume and they were satisfied. Okay, he wants that this food. So then the question is, even student, uh, during ane of the semester, the selected at random and admits having been satisfied with the textbook is the educatee most likely to have used book by men median On what instance? Or to figure out that we're going to investigate one at a time. And then what is the probability or the hazard? Ah, that the educatee had used means book her means they're using ways book. Okay, given that they are satisfied with it. And this will be total number of strands who used to Maine's volume and was satisfied, which is 200 divided past. Nosotros demand to notice the total number of students who are satisfied, which was 500 and 491 of satisfied. Okay, then we're going to split up this by 510. This gives apply every kind 3 and nine, and and then we go to the next ane probability, Simply this Didn't he used, uh, fabricated Ian's book? Okay, Probability used a made Ian's book. Okay. Okay. Having been satisfied, given that they will satisfy, this will be 100 on 50 divided by 510 which is a little backside 3. And then nothing signal took not three little betoken 2919494 So finally, what is a chance that the student are the years to mourns? Textbook having beingness satisfied it And these will be 160 divided by 510 which is zero signal 313 So if you lot look at these results, yous realize that, um, information technology is more probable that the pupil had to use what he's more probable. No. The educatee used, uh, professor means textbook. Okay, Considering, as you can see, the chance is 3 continental and the over who is least probable the to the lowest degree likely author is, as you tin see, he'south professor media to the lowest degree likely. All the is professor motion-picture show because yous can see the probability of using his volume. Having been satisfied with it. He's on the 0.29 for and that'due south the finish of information technology. Okay. Thanks. Watching
Similar Solved Questions
one answers
In Problems $xi-22,$ use $U=$ universal ready $=\{0,i,ii,3,4,5,half-dozen,7,8,nine\}, A=\{one,3,4,v,9\}, B=\{2,4,6,seven,8\},$ and $C=\{ane,3,iv,half dozen\}$ find each set. $$ (A \cup B) \cap C $$
In Issues $11-22,$ use $U=$ universal set $=\{0,1,2,3,4,five,half dozen,7,eight,9\}, A=\{1,3,iv,5,9\}, B=\{2,4,six,seven,viii\},$ and $C=\{ane,iii,four,vi\}$ find each set. $$ (A \cup B) \cap C $$...
Source: https://itprospt.com/num/14909153/textbook-authors-must-be-careful-that-the-reading-level
0 Response to "Textbook Authors Must Be Careful That the Reading Level"
Post a Comment